ANSWER
a) 150ft
b) 3.05s
EXPLANATION.
The quadratic function that models the height of the ball is
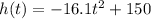
The ball was dropped at time t=0.
We plug in t=0 into the given function to get,
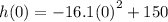
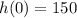
Therefore the ball was dropped from a height of 150 ft.
When the ball hit the ground, then h(t)=0.
This implies that:

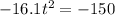
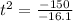
We take square root of both sides,
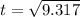
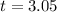 to the nearest hundredth.
to the nearest hundredth.
Therefore the ball hit the ground after approximately 3.05 seconds.