Question

three times a number is subtracted from another number and the difference is 3. The sum of the two numbers is 31. What is the smaller of the two numbers

Answer 1

Answer: The two numbers are 7 and 24. The smaller of the two numbers is 7

Explanation:

Let the two numbers be x and y

The mathematical interpretation of the first statement (three times a number is subtracted from another number and the difference is 3) is y - 3x = 3

For the second statement ( the sum of the two numbers is 31), its mathematical interpretation is x+ y = 31

from y = 31 - x

we can substitute y in the equation y - 3x = 3

(31 - x) - 3x = 3

Then we can now proceed and solve for x

31 - x -3x = 3

31 - 4x = 3 subtract 31 from both-side of the equation

31 - 31 - 4x = 3 - 31

-4x = -28

Divide both-side of the equation by -4

`(-4x)/(-4) = (-28)/(-4)`

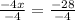
x = 7

substituting x = 7 in y = 31 - x

y = 31 - 7 = 24

x= 7 and y = 24

The two numbers are 7 and 24

Therefore the smaller number is 7

Answer 2

The smaller number is 7.

EXPLANATION

Let the numbers be x and y.

Then we have;

y-3x=3... eqn (1)

If the sum of the numbers is 3 then,

y+x=31... eqn (2)

Eqn(2) - Eqn (1)

x--3x=31-3

`4x = 28`

Divide both sides by 4,

`x = 7`

We put x=7 into the second equation,

y+7=31

y=31-7

y=24

The smaller of the two numbers is 7.