Answer:
The area of rectangle is
 .
.
Explanation:
Given that,
Length of rectangle =
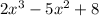
Width of rectangle =
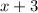
Area of rectangle = A = ?
Area of a rectangle is calculated by multiplying length with width
A = l * w
In our case

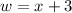
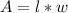
=>
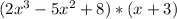
=>
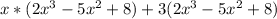
=>

=>
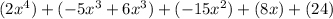
=>
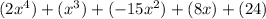
=>

Therefore, the area of rectangle is
 .
.