Question

Find the surface area of the composite solid.

A.
680 in.2
B.
800 in.2
C.
920 in.2
D.
1,040 in.2

Answer 1

The ends of the rectangle = 10*10*2 = 200

The long sides and bottom of the rectangle = 12*10*3 = 360

Vertical end of the triangle = 5*10 = 50

The sides of the triangle = 12*5*1/2*2 = 60

Triangle slope = 13*10 = 130

Total = 200 + 360 + 50 + 60 + 130 =

800 in sq

Answer 2

Option B. 800 in²

Explanation:

We have to find the surface area of the composite solid.

This solid is made up of two solids, Rectangular prism and a right angle triangular prism.

Now we will calculate surface area separately.

Surface area of rectangular prism = 2(lw + hl + hw)

But one side of lw is hidden so formula will be = 2(lw +hl + hw) - lw

where h = height = 10 in

w = width = 12 in

l = length = 10 in

Surface area of rectangular prism = 2(10×12 + 10×10 + 10×12) - 10×12

= 2(120 + 100 + 120) - 120

= 2(340) - 120 = 560 in²

Surface area of right angle triangular prism = 2(Rectangle sides)+ 2(triangular sides)

Surface area of triangular prism = 5×10 + 13×10 + 2(
`(1)/(2))(5)(12)`

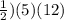
= 50 + 130 + 60

= 240 in²

Now total surface area of the composite solid = surface area of rectangular prism + surface area of triangular prism

= 560 + 240 = 800 in²

Therefore, option B. 800 in² is the answer.