Question

What is the best approximation of the projection of (5, -1) onto (2, 6)

A. 0.10(5, -1)
B. 0.10(2, 6)
C. 0.15(2,6)
D.0.15(5. -1)

Answer 1

Answer with explanation:

Suppose we represent ordered pairs in terms of vectors.

`\vec{A}`

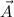
Ordered pair of points , (5,-1) in terms of vectors is represented by = 5 i - j

`\vec{B}`

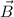
Ordered pair of points , (2,6) in terms of vectors is represented by =2 i + 6 j

Projection of Vector A on Vector B

`\frac{(\vec{A}.\vec{B})(\vec{B})}{|\vec{B}|^2}\\\\=([(5i-j).(2 i+6 j)](2 i+6 j))/(√(2^2+(6)^2))\\\\=((10-6)(2 i+6 j))/(√(40))\\\\=(4)/(6.325)* (2i+6j)\\\\=0.6324* (2 i+ 6j)`

= 0.6324 (2,6)

Answer 2

B. 0.10(2, 6)

Explanation:

A careful graph of the vectors can help you answer this question. The end point of the projection of (5, -1) onto (2, 6) is (0.2, 0.6) = 0.10(2, 6).