Question

Identify the vertex of y=-1(x-4)^2+9 and tell whether it’s a minimum or maximum

Answer 1

Answer: option B

Explanation:

Given the quadratic equation
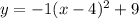`y=-1(x-4)^2+9`, you can use the formula to find the x-coordinate of the vertex of the parabola:

`x=(-b)/(2a)`

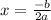
Simplify the quadratic equation. Remember that:

`(a-b)^2=a^2-2ab+b^2`

Then:

`y=-1(x-4)^2+9\\y=-1(x^2-2(x)(4)+4^2)+9\\y=-x^2+8x-16+9\\y=-x^2+8x-7`

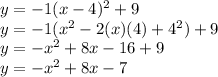
Substituting:

`x=(-8)/(2(-1))=4`

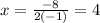
The y-coordinate is:

`y=-(4)^2+8(4)-7=9`

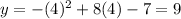
The vertex is at (4,9) therefore it is a maximum.

Answer 2

B. (4,9), maximum

Explanation:

The given function is

`y=-1(x-4)^2+9`

This function is of the form;

`y=a(x-h)^2+k`

where (h,k)=(4,9) is the vertex.

and
`a=-1` since 'a' is negative the vertex is the maximum point on the graph of this function.

The correct answer is B