Question

Can someone help me figure this out?

Answer 1

a.
`f(x)=x^2-5x-24`

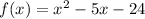
b. (2.5,-30.25) is the vertex

c. The x-intercepts are (-3,0) and (8,0)

d. See graph

Explanation:

a. The given function is;

`f(x)=x^2-5x-24`

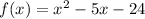
We complete the square to obtain;

`f(x)=x^2-5x+(-(5)/(2))^2 -(-(5)/(2))^2 -24`

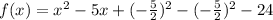
Observe that the first three term is a perfect square trinomial.

`f(x)=(x-(5)/(2))^2 -30.25`

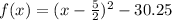
This is the same as

`f(x)=(x-2.5)^2 -30.25`

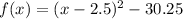
b.

The function is now of the form;

`f(x)=a(x-h)^2+k`

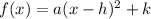
Where (h,k)=(2.5,-30.25) is the vertex.

c.

At x-intercept, y=0

This implies that;

`(x-2.5)^2 -30.25=0`

`(x-2.5)^2 =30.25`

`x-2.5=\pm √(30.25)`

`x=2.5\pm 5.5`

`x=2.5\pm 5.5`

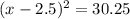
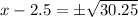
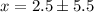
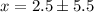
`x=-3` or
`x=8`

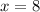
The x-intercepts are (-3,0) and (8,0)

At y-intercept x=0,

This implies that;

`f(0)=0^2-5(0)-24=-24`

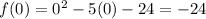
The y-intercept is (0,-24)

d) We now plot the vertex (2.5,-30.25).

The a=1, this means the graph opens upwards.

We also plot the intercepts and graph the function to obtain the graph shown in the attachment.

Answer 2

a)
`y = (x-(5)/(2)) ^ 2 -(121)/(4)`

b)
`((5)/(2), -(121)/(4))`

c)
`x = 8`,
`x = -3`
`y=-24`

d) Observe the attached image.

Explanation:

The function is:

`x ^ 2 -5x -24`

We want to write this parable in its vertex form

`a(x-h) ^ 2 + k`

By definition the vertex of a parabola of the form
`ax ^ 2 + bx + c` is given by the equation

`x = -(b)/(2a)`

In this case

`a = 1\\b = -5\\c = -24`

Then the vertice is:

`x = (5)/(2(1))`

`x = (5)/(2)`

Then
`h =(5)/(2)`

`k = (2.5) ^ 2 -5 (2.5) -24\\\\k = -(121)/(4)`

Then the equation written in its vertex form is:

`y = (x-(5)/(2)) ^ 2 -(121)/(4)`

Then the intercept in y we determine it by doing x = 0

`y = 0 ^ 2 -5 (0) -24\\\\y = -24`

The intercept in x is determined by doing y = 0 and solving for x.

`0 = (x-(5)/(2)) ^ 2 -(121)/(4)\\\\(x-(5)/(2)) ^ 2 = (121)/(4)\\\\(x-(5)/(2)) = \sqrt{(121)/(4)}\\\\x_1 = (11)/(2) +(5)/(2) = 8\\\\x_2 = -(11)/(2) +(5)/(2) = -3`

The intercepts with the x axis are in the points

`x = 8`,
`x = -3`