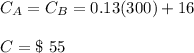Question

A phone company offers two monthly plans. Plan A costs $16

plus an additional $0.13 for each minute of calls. Plan B costs $28 plus an additional $0.09 for each minute of calls.

For what amount of calling do the two plans cost the same? ______ minutes

What is the cost when the two plans cost the same? $ ________

Answer 1

Explanation:

Answer 2

For what amount of calling do the two plans cost the same? __300__ minutes

What is the cost when the two plans cost the same? $ __55__

Explanation:

We have 2 plans, A and B. We must find an equation that relates the cost of the plan based on the number of minutes of calls.

For plan A we have:

Fixed cost of $ 16.

Variable cost of 0.13(m)

Where m represents the minutes of additional calls.

Then the equation for the cost
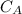`C_A` is:

`C_A = 0.13m + 16`

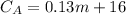
For plan B we have:

Fixed cost of $28.

Variable cost of 0.09(m)

Where m represents the minutes of additional calls.

Then the equation for the cost
`C_B` is:

`C_B = 0.09m + 28`

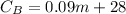
To find out when the plans cost the same, we must equalize both equations and solve for m:

`C_A = C_B\\\\0.13m + 16 = 0.09m + 28\\\\0.04m = 12\\\\m = 300\ minutes.`

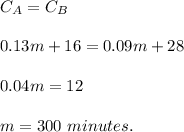
When the number of additional minutes is 300 the costs of the plans are equal to:

`C_A = C_B = 0.13(300) + 16\\\\C = \$\ 55`