Question

Without using log, Solve for x.


`25^(2x+3) = 125^(x)`

Answer 1

x=-6

Explanation:

The given exponential equation is;

`25^(2x+3)=125^x`

Rewrite both sides to base 5.

`5^(2(2x+3))=5^(3x)`

Equate the exponents;

`2(2x+3)=3x`

Expand:

`4x+6=3x`

Group like terms;

`4x-3x=-6`

Simplify

`x=-6`

Answer 2

x = -6

Explanation:

We recognize that 25 = 5^2 and also 125 = 5^3, thus we can write:

`25^(2x+3)=125^x\\(5^2)^(2x+3)=(5^3)^x`

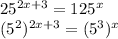
Now we can use the property of exponents [
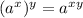`(a^x)^y=a^(xy)`] to simplify it:

`(5^2)^(2x+3)=(5^3)^x\\5^(2(2x+3))=5^(3x)\\5^(4x+6)=5^(3x)`

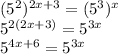
We equate the exponents (since we have similar base) to find the value of x:

4x + 6 = 3x

4x - 3x = -6

x = -6