Answer:
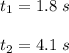
Explanation:
If the equation
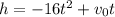 represents the position of the ball as a function of time then, to find in which second the ball reaches 120 feet must substitute
represents the position of the ball as a function of time then, to find in which second the ball reaches 120 feet must substitute
 in the equation of the height and solve for t.
in the equation of the height and solve for t.

If the initial velocity is 95 feet/s then
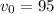
Then:
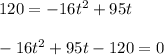
Use the quadratic formula

Where, for this problem:
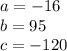
So
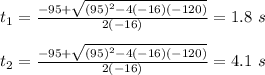
This result means that the ball reaches 120 feet for the first time at 1.8 seconds, then begins to descend and on its descent again reaches 120 feet at t = 4.1 seconds.