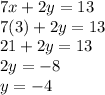Question

Solve the system using subtraction. 7x + 2y = 13 –x + 2y = –11 What is the solution of the system?

Answer 1

`x=3\\y=-4`

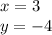
Explanation:

Subtract both equations:

`(7x+2y)-(-x+2y)=13-(-11)`

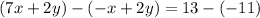
Distribute the negative signs and then you need to add the like terms:

`7x+2y+x-2y=13+11\\8x=24`

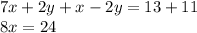
BY the division prperty of equality, divide both sides of the equation by 8:

`(8x)/(8)=(24)/(8)\\x=3`

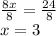
Substitute the value of x obtained into any of the original equations to find the value of y. Then you get:

`7x+2y=13\\7(3)+2y=13\\21+2y=13\\2y=-8\\y=-4`

Answer 2

ANSWER

The solution is

x=3, y=-4

EXPLANATION

We were given two equations in two variables.

First equation:


`7x + 2y = 13`

Second equation:


`- x + 2y = - 11`

Subtract the second equation from the first equation:


`(7x - - x) + (2y - 2y) = 13 - - 11`

This gives us,


`7x + x + 0= 13 + 11`


`8x= 24`

Divide both sides by 8.


`x = (24)/(8)`


`x = 3`

Put x=3 into the first equation:


`7(3) + 2y = 13`


`21 + 2y = 13`

Group similar terms;


`2y = 13 - 21`


`2y = - 8`

Divide both sides by 2,


`y = ( - 8)/(2) = - 4`

The solution is

x=3, y=-4