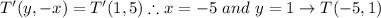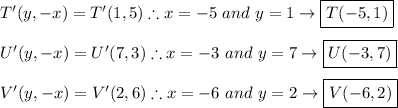Question

Crystal is amazed! She graphed ΔABC using the points A(5, –1), B(3, –7), and C(6, –2). Then she rotated ΔABC 90° counterclockwise (↺) about the origin to find ΔA′B′C′. Meanwhile, her teammate took a different triangle (ΔTUV) and rotated it 90° clockwise (↻) about the origin to find ΔT′U′V′. Amazingly, ΔA′B′C′ and ΔT′U′V′ ended up having exactly the same points! Name the coordinates of the vertices of ΔTUV.

Answer 1

Crystal graphed ΔABC using the following points:

`A(5, -1) \\ \\ B(3, -7) \\ \\ C(6, -2)`

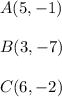
On the coordinate plane, consider the point
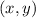`(x,y)`. To rotate this point by 90° around the origin in counterclockwise direction, you can always swap the x- and y-coordinates and then multiply the new x-coordinate by -1. In a mathematical language this is as follows:

`(x,y)\rightarrow(-y,x)`

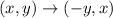
Therefore, for ΔA′B′C′ we have:

`\boxed{A'(1, 5)} \\ \\ \boxed{B'(7, 3)} \\ \\ \boxed{C'(2, 6)}`

Since ΔA′B′C′ and ΔT′U′V′ ended up having exactly the same points, then:

`T'(1, 5) \\ \\U'(7, 3) \\ \\V'(2, 6)`

On the other hand, in clockwise direction we have the following rule:

`(x,y)\rightarrow(y,-x)`

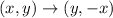
Therefore. we must find
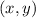`(x,y)` to get ΔTUV here, so:

`T'(y,-x)=T'(1, 5) \therefore x=-5 \ and \ y=1 \rightarrow T(-5,1)`

`T'(y,-x)=T'(1, 5) \therefore x=-5 \ and \ y=1 \rightarrow \boxed{T(-5,1)} \\ \\U'(y,-x)=U'(7, 3) \therefore x=-3 \ and \ y=7 \rightarrow \boxed{U(-3,7)} \\ \\V'(y,-x)=V'(2, 6) \therefore x=-6 \ and \ y=2 \rightarrow \boxed{V(-6,2)}`