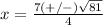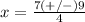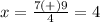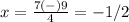Question

Question 1- explain how Sheldon immediately knew howard was incorrect?

question 2- identify where Howard made a mistake in his work?​

Answer 1

Part 1) In the procedure

Part 2) In the procedure

Explanation:

Part 1) Observing the graph

The roots are x=-1/2 and x=4

Remember that, the roots are the x-values when the value of y is equal to zero (the x-intercepts)

That's why Sheldon immediately realizes Howard's solution is incorrect

Part 2) we have

`y=2x^(2)-7x-4`

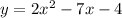
The formula to solve a quadratic equation of the form
`ax^(2) +bx+c=0` is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

in this problem we have

equate the equation to zero

`2x^(2)-7x-4=0`

so

`a=2\\b=-7\\c=-4`

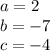
substitute

`x=\frac{-(-7)(+/-)\sqrt{-7^(2)-4(2)(-4)}} {2(2)}`

`x=\frac{7(+/-)√(49+32)} {4}`

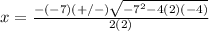
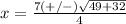
Howard's error is in this step, is wrong with the sign of the number 7, is positive instead of negative

`x=(7(+/-)√(81))/(4)`

`x=(7(+/-)9)/(4)`

`x=(7(+)9)/(4)=4`

`x=(7(-)9)/(4)=-1/2`