Question

A fisherman notices that his boat is moving up and down periodically, owing to waves on the surface of the water. It takes 2.5 s for the boat to travel from its highest point to its lowest, a total distance of 0.53 m. The fisherman sees that the wave crests are spaced 4.8 m apart. (a) How fast are the waves traveling? (b) What is the amplitude of each wave? (c) If the total vertical distance traveled by the boat were 0.30 m but the other data remained the same, how would the answers to parts (a) and (b) change?

Answer 1

(a) 0.96 m/s

The period of the wave corresponds to the time taken for one complete oscillation of the boat, from the highest point to the highest point again. Since the time between the highest point and the lowest point is 2.5 s, the period is twice this time:

`T=2\cdot 2.5 s=5.0 s`

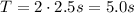
The frequency of the waves is the reciprocal of the period:

`f=(1)/(T)=(1)/(5.0 s)=0.20 Hz`

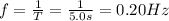
The wavelength instead is just the distance between two consecutive crests, so

`\lambda=4.8 m`

And the wave speed is given by:

`v=\lambda f=(4.8 m)(0.20 Hz)=0.96 m/s`

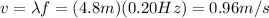
(b) 0.265 m

The total distance between the highest point of the wave and its lowest point is

d = 0.53 m

The amplitude is just the maximum displacement of the wave from the equilibrium position, so it is equal to half of this distance. So, the amplitude is

`A=(d)/(2)=(0.53 m)/(2)=0.265 m`

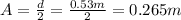
(c) Amplitude: 0.15 m, wave speed: same as before

In this case, the amplitude of the wave would be lower. In fact,

d = 0.30 m

So the amplitude would be

`A=(d)/(2)=(0.30 m)/(2)=0.15 m`

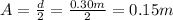
Instead, the wave speed would not change, since neither the frequency nor the wavelength of the wave have changed.