Question

If a particle's position is given by x = 4 − 12 t + 3 t^ 2 (where t is in seconds and x is in meters), what is its velocity at s t = 1 s ? b) Is it moving in the positive or negative direction of x just then? c) What is its speed just then? d) Is the speed increasing or decreasing just then? (Try answering the next two questions without further calculations.) e) Is there ever an instant when the velocity is zero? If so, give the time t ; if not, answer no. f) Is there a time after t = 3 s when the particle is moving in the negative direction of x ? If so, give the time t ; if not, answer no.

Answer 1

a) -6 m/s

The particle's position is given by

`x=3t^2-12t+4`

where t is the time.

The velocity of the particle can be found by calculating the derivative of the particle's position with respect to the time:

`v=x'(t)=3(2t)-12=6t-12`

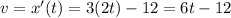
So, the velocity at instant t=1 can be found by substituting t=1 in this formula:

`v(1 s)=6(1)-12=-6 m/s`

b) Negative direction

At instant t=1 second, the particle's velocity is

`v=-6 m/s`

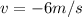
we see that this velocity is negative: therefore, this means that the particle is moving along the negative x-direction.

c) 6 m/s

The particle's speed is just equal to the magnitude of the velocity:

`speed = |v|`

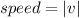
Since the speed is a scalar and velocity is a vector.

Since the velocity is

`v=-6 m/s`

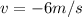
Then, the speed of the particle is

`speed = |-6 m/s| = 6 m/s`

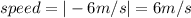
d) Increasing

The speed is the magnitude of the velocity, so we can write

`speed = |v| = |6t-12|`

We notice that at t = 1 s, for little increments of t the term (6t) is increasing in magnitude, while the constant term -12 remains constant. This means that the whole function

`|6t-12|`

is increasing at t=1 s, so the speed is increasing.

e) yes, at t = 2 s

In order to find an instant in which the velocity is zero, we just need to set v(t)=0 in the equation:

`6t-12 =0`

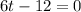
and solving the equation for t, we find

`6t=12\\t=(12)/(6)=2`

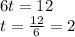
So, at t = 2 seconds the velocity is zero.

f) No

The particle is moving in the negative direction of x when the velocity vector v(t) is negative.

The velocity vector is

`v(t) = 6t -12`

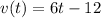
we see that at t=3 s, it is equal to

`v(3) = 6(3)-12 = 18-12=+6`

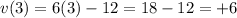
so it is positive.

For every time t > 3 s, we notice that the term (6t) in the formula is increasing and always positive, and since it is always larger than the constant negative term (-12), we can conclude that the velocity is always positive for every time > 3 seconds.