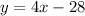Question

Write an equation of a line that passes through the point (8,4) and is parallel to the y=4x+2

Answer 1

Answer:
`y=4x-28`

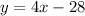
Explanation:

The Slope-intercept form of the equation of the line is:

`y=mx+b`

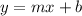
m: is the slope.

b: the intersection of the line with the y-axis.

The equation of the line
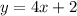`y=4x+2` has:

`m=4\\b=2`

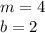
If both lines are parallel, then their slopes are equal. So the slope of the other line is:

`m=4`

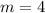
To find "b", substitute the given point and the slope into
`]y=mx+b` and solve for "b":

`4=4(8)+b\\4-32=b\\b=-28`

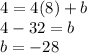
Then the equation of this line is:

`y=4x-28`