Question

Steve determines that sides DK and BC are congruent. He also measures angle K and angle C and determines that

they are congruent. He concludes that the triangles are congruent by the SAS Congruence Theorem. Is Steve correct?

If he is incorrect, which congruence theorem should Steve use? Explain your reasoning

Answer 1

Answer and Step-by-step explanation: Two triangles are congruent when they have the same 3 sides and the same 3 angles.

One way to find if they are congruents is a theorem called "Side-Angle-Side" (SAS): if two sides and its included angle is equal to the other triangle's corresponding sides and angles, the triangles are congruent.

In the graph below, in triangle DEK, as Steve determined, side DK measures 12. In triangle ABC, side BC is also 12. The angles K and C are equals, so if sides EK and AC are congruent, SAS Congruent Theorem is correct.

To test it, find distances EK and AC, which is calculated as:

`d=\sqrt{(x_(1)-x_(2))^(2)-(y_(1)-y_(2))^(2)}`

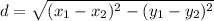
EK is a distance between points E(-6,4) and K(0,-4)

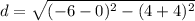`d=\sqrt{(-6-0)^(2)-(4+4)^(2)}` = 10

AC is a distance between points A(3,6) and C(9,-2)

`d=\sqrt{(3-9)^(2)-(6+2)^(2)}` = 10

EK and AC have the same distances between each point, i.e., segment EK measures the same as segment AC, 10 units.

Therefore, triangles DEK and BAC are congruent proven by SAS Congruence Theorem.