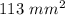Question

A circle fits inside a semicircle of diameter 24mm

Calculate the shaded area
Give your answer to 3 significant figures and state its units​

Answer 1

113mm^2

Explanation:

π×6²=113.097336

π×12²=452.389342

452.389342÷2=226.194671

226.194671-133.097336=113.097335

rounded to 3 s.f 113mm^2

Answer 2

The shaded are is
`113\ mm^(2)`

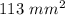
Explanation:

we know that

The shaded area is equal to the area of the semicircle minus the area of the circle inside the semicircle

step 1

Find the area of semicircle

The area of semicircle is equal to

`A=(1)/(2)\pi r^(2)`

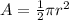
where

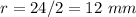`r=24/2=12\ mm` ----> the radius is half the diameter

substitute

`A=(1)/(2)\pi(12)^(2)=72\pi\ mm^(2)`

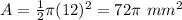
step 2

Find the area of the circle inside the semicircle

The area of circle is equal to

`A=\pi r^(2)`

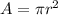
where

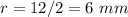`r=12/2=6\ mm` ---> the radius of circle inside is half the radius of semicircle

substitute

`A=\pi(6)^(2)=36\pi\ mm^(2)`

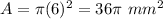
step 3

Find the shaded area

`72\pi\ mm^(2)-36\pi\ mm^(2)=36\pi\ mm^(2)`

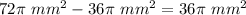
assume

`\pi=3.14`

`36(3.14)=113.04\ mm^(2)`

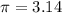
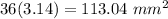
3 significant figures is

`113\ mm^(2)`