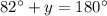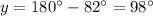Question

A quadrilateral is inscribed in a circle. Find the measure of each of the angles of the quadrilateral. Show your work and/or explain how you got your answer.

m∠z=

I know this because…

m∠x=

I know this because…

m∠y=

I know this because…

Answer 1

Part 1) The measure of angle Z is
`87\°`

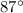
Part 2) The measure of angle x is
`82\°`

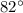
Part 3) The measure of angle y is
`98\°`

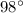
Explanation:

we know that

In a inscribed quadrilateral opposite angles are supplementary

so

In this problem

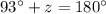`93\°+z=180\°` ------> equation A

`x+y=180\°`----> equation B

step 1

Find the measure of angle Z

Solve the equation A

`93\°+z=180\°`

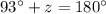
solve for z

`z=180\°-93\°=87\°`

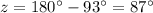
step 2

Find the measure of angle x

we know that

The inscribed angle is half that of the arc it comprises.

so

`m<x=(1)/(2)(58\°+106\°)= 82\°`

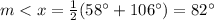
step 3

Find the measure of angle y

Solve the equation B

`x+y=180\°`

we have

`x=82\°`

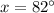
substitute

`82\°+y=180\°`

`y=180\°-82\°=98\°`