Question

Need help with geometry

Answer 1

The surface area is
`305.9\ ft^(2)`

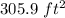
Explanation:

we know that

The surface area of the square pyramid is equal to

`SA=b^(2)+4[(1)/(2)bh]`

where

b is the length side of the square base

h is the height of the lateral triangular face

we have

`b=10\ ft`

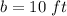
Applying Pythagoras Theorem find the value of h

`h^(2)=9^(2)+(10/2)^(2)`

`h^(2)=81+25`

`h=√(106)\ ft`

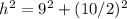
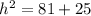
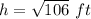
substitute in the formula

`SA=10^(2)+4[(1)/(2)(10)(√(106))]=305.9\ ft^(2)`