Question

The length of a rectangle is represented by the polynomial 2x3 – 5x2 + 8 and the width is represented

by the polynomial x + 3. Complete the following statements about the polynomial that represents the
area of the rectangle.
​

Answer 1

2 square units

Explanation:

We know that the area of a rectangle is:

`A=(length)(width)`

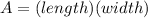
And, givens are:

`length=2x^(3) -5x^(2)+8\\width=x+3`

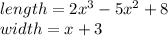
Replacing given expression:

`A=(2x^(3) -5x^(2)+ 8)(x+3)`

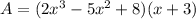
So, to find the area, we need to solve that expression. The faster and easier way to do it is by graphing, given values to x-variable, and finding values for y-variable in return. Each pair represents a point. The graph is like the image attached.

In the graph, we observe that only has two solutions:

`(-3,0) (-1.06;0)`

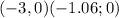
Now, we test each one to find an area that make sense, that is, a positive area:

`length=2(-3)^(3) -5(-3)^(2)+ 8\\width=-3+3=0`

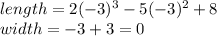
We see that -3 makes the width zero, which don't make sense. So, we use -1.06, or just -1.

`length=2(-1)^(3) -5(-1)^(2)+ 8=-2-5+8=1\\width=-1+3=2`

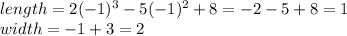
Therefore, the area is A=(2)(1)=2 square units

Answer 2

1) the polynomial representing the area is

2x^4 + 6x^3 - 5x^2 -7x + 24

2) the constant term is

24

3) the polynomial is a 4th degree

4) if my guess is ryt... the LEADING coefficient is the coefficient of the highest degree of X ...i.e 2