Answer:
The standard form of the equation of the parabola is
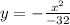 .
.
Explanation:
The general form of a parabola is
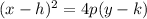
Where, (h,k) is vertex, (h,k+p) is focus and y=k-p is directrix.
Focus of the parabola is (0, -8).
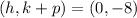
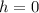
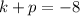 .... (1)
.... (1)
Directrix of the parabola is
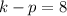 .... (2)
.... (2)
On adding (1) and (2) we get
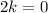
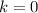
Put this value in equation (1).
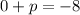
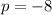
The value of p is -8.
Substituent h=0,k=0 and p=-8 in general form of parabola.
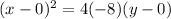

Divide both sides by -32.
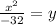
Therefore the standard form of the equation of the parabola is
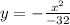 .
.