Question

A graph of 2 functions is shown below.

graph of function f of x equals 2 multiplied by x plus 1 and graph of function g of x equals x cubed plus 2 multiplied by x squared minus x minus 2

Which of the following is an approximate solution for f(x) = g(x)?


A) x = −2
B) x = 0
C) x = −1
D) x = 1

Answer 1

Answer: x=-1

Explanation:

Both lines cross -1 on the x axis and I got it right on my test

Answer 2

The approximate solution for f(x)=g(x) is x= -1.

Explanation:

Given two functions are f(x) and g(x)

f(x)=
`2 \;multiplied \;by \;x\; plus 1`

Therefore, f(x)= 2x+1

g(x)=
`x\; cubed\; plus \; 2\; multiplied\; by \; x \; squared \; minus \; x\; minus2`

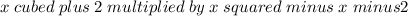
Therefore, g(x)=
`x^3+2x^2-x-2`

From the given graph we can see that two functions are intersect to each other at points (1.46, 3.92) , ( -0.76, -0.52) and ( -2.7,-4.3).

It means the graph of two functions intersect at

x=1.46

x= -0.76

x=-2.7

The approximate value of

x=1.46=1.5

x=- 0.76=-1

x=-2.7=-3

Hence, f(x)=g(x) at x=-1

Therefore , the approximate solution is x= -1 for f(x)=g(x)

Hence, option C x=-1 is correct answer.