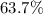Answer:
Explanation:
we know that
To find the percent divide the area of the square by the area of the circle
step 1
Find the area of the circle
The area of the circle is
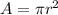
we have
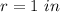
substitute the values
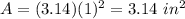
step 2
Find the area of the square
The area of the square is
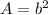
where
b is the length side of the square
we have
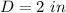 ---> the diagonal of the square is equal to the diameter of the circle
---> the diagonal of the square is equal to the diameter of the circle
Applying Pythagoras Theorem
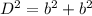
substitute the values
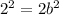
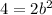
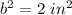 ------> the area of the square
------> the area of the square
step 3
Find the percent
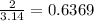
Convert to percent
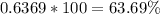
Round to the nearest tenth of a percent