Question

Determine the small gravitational force F which the copper sphere exerts on the steel sphere. Both spheres are homogeneous, and the value of r is 65 mm. Express your result as a vector.

Answer 1

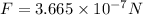`F=3.665 * 10^(-7) N` acting along the line joining both the sphere and always attractive in nature.

Step-by-step explanation:

The given radius of both the sphere, r= 65 mm = 0.065 m

So, the volume of the spheres,
`v= \frac 4 3 \pi r^3`

`v= \frac 4 3 \pi (0.065)^3 = 1.150 * 10^(-3) m^3`

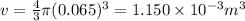
The density of steel,
`\rho _s = 7850 kg/m^3`

and the density of copper,
`\rho_c= 8940 kg/m^3`

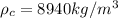
Let M be the mass of the copper ball and m is the mass of the steel ball.

So,
`M=\rho_c v= 8940* 1.150 * 10^(-3) = 10.281` kg

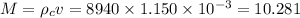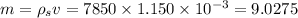`m=\rho_s v= 7850* 1.150 * 10^(-3) = 9.0275` kg

The gravitational force, F, between the two objects having masses M and m and separated by distance d is

`F=(GMm)/(d^2)`

Where
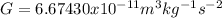`G= 6.674 30 x 10^(-11) m^3 kg^(-1) s^(-2)` is the universal gravitational constant.

When both the sphere touches each other, d = 2r= 2 x 0.065 = 0.13 m

Hence, the gravitational force between both the sphere,

`F= \frac {6.674 30 x 10^(-11)* 10.281 * 9.0275}{0.13^2} \\\\F=3.665 * 10^(-7) N`

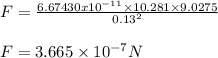
The nature of gravitational force is always attractive and acting along the line joining the center of both the sphere.