Answer:
A) AB = 24 and DE = 12
Explanation:
If two triangles have two pairs of sides in the same ratio and the included angles are also equal, then the triangles are similar. Then:
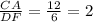
On the other hand:
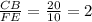
So, the additional fact that would guarantee that the the triangles are similar is AB=24 and DE=12 given that:
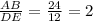
So the three pairs of sides have the same ration, in consequence, the angles are also equal.