Question

Which set of points contains the solutions to the equation y = –4⁄3x – 7⁄3?

A. {(3,–19), (2,3), (8,26)}
B. {(–3,–17), (4,11), (3,19)}
C. {(2,–5), (5,–9), (29,–41)}
D. {(–2,–18), (9,–61), (5,15)}

Answer 1

C. {(2,–5), (5,–9), (29,–41)}

Explanation:

we have

`y=-(4)/(3)x-(7)/(3)`

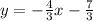
The slope of the given line is
`m=-(4)/(3)`

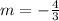
we know that

If a set of ordered pairs is a solution of the given line

then

the slope between two points of the set must be equal to
`m=-(4)/(3)`

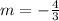
The formula to calculate the slope between two points is equal to

`m=(y2-y1)/(x2-x1)`

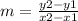
Verify each case

case A) {(3,–19), (2,3), (8,26)}

`m=(26-3)/(8-2)`

`m=(23)/(6)`

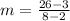
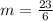
so

`(23)/(6)\\eq-(4)/(3)`

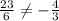
The set of case A) is not a solution of the given line

case B) {(–3,–17), (4,11), (3,19)}

`m=(19-11)/(3-4)`

`m=-8`

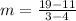
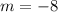
so

`-8\\eq-(4)/(3)`

The set of case B) is not a solution of the given line

case C) {(2,–5), (5,–9), (29,–41)}

`m=(-9+5)/(5-2)`

`m=-(4)/(3)`

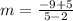
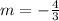
so

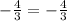`-(4)/(3)=-(4)/(3)` ----> is true

Verify if the third point satisfy the equation of the given line

(29,–41)

`-41=-(4)/(3)(29)-(7)/(3)`

`-41*3=-123`

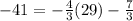
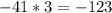
`-123=-123` ------> is true

therefore

The set of case C) is a solution of the given line

case D) {(–2,–18), (9,–61), (5,15)}

`m=(15+61)/(5-9)`

`m=-(76)/(4)`

`m=-19`

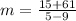
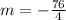
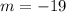
so

`-19\\eq-(4)/(3)`

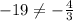
The set of case D) is not a solution of the given line