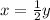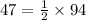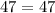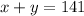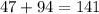Question

One number is half another number. The sum of the two numbers is 141. Find the numbers.

Restate the applied problem.

You must translate the words into a system of equations for solving the problem.

Solve the system of equations for the answers. You must provide detailed step-by-step explanations on how you solved the problem.

Explain in detail how you would check your answers.

Answer 1

x = 47

y = 94

Explanation:

We know that one number is half another number and the sum of these two numbers is 141. We are to find the numbers.

Assuming
`x` and
`y` to be the numbers, we can write it as:

`x=(1)/(2)y` --- (1)

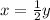`x+y=141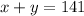` --- (2)

Substituting the value of
`x` from (1) into (2) to get:

`(1)/(2)y+y=141`

`(3)/(2)y+y=141`

`y=141 * (2)/(3)`

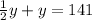
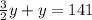
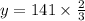
y = 94

Now substituting this value of
`y` in (1):

`x=(1)/(2) * 94`

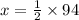
x = 47

Translating it in other words:

One number is double the other number and the sum of the two number is 141.

Checking answers:

`x=(1)/(2)y`

`47=(1)/(2) * 94`

`47=47`

`x+y=141`

`47+94=141`

Answer 2

x = 47

y = 94

Explanation:

Givens

Let the larger number = y Note: y must be even. Why is that?

Let the smaller number = x

Equations

x = 1/2 y

x + y = 141

Solution

Substitute x from the first equation into the second equation

1/2 y + y = 141

Change 1/2 y to 0.5y

0.5y + y = 141

Combine the left

1.5y = 141

Divide both sides by 1.5

1.5y/1.5 = 141/1.5

Do the division

y = 94 And y is even.

================

x = 1/2y

x = 1/2*94

x = 47

Check

The smaller number is 1/2 the larger one This is correct.

47 + 94 = 141 and this also checks.