Question

A 0.0469 kg ingot of metal is heated to 213◦c and then is dropped into a beaker containing 0.401 kg of water initially at 22◦c. if the final equilibrium state of the mixed system is 24.4 ◦c, find the specific heat of the metal. the specific heat of water is 4186 j/kg · ◦

c. answer in units of j/kg · ◦

c.

Answer 1

455 J/kg°C

Step-by-step explanation:

Assuming that no heat is dissipated out of the system, we can use the specific heat formula to solve for the specific heat of the ingot. The system is in thermal equilibrium and assume that all heat dissipated from the ingot is transferred to the water.

Here's the equation for specific heat:

Q = smΔT

Q is energy, s is the specific heat, m is mass and ΔT is the change in temperature. Units are J, J/(kg*°C), kg, °C respectively.

Since we know heat energy is conserved, we can set the ingot energy loss to the water energy gain. This yields: (d is the same as Δ)

`s_(ingot)*m_(ignot)*dT_(ingot) = s_(water)*m_(water)*dT_(water)\\`

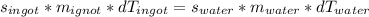
Substitute the values we know, we get:

`s_(ingot)*0.0469kg*(213-24.4)C=4186(J)/(kg*C)*0.401kg*(24.4-22)C\\s_(ingot) = 455.4495814(J)/(kg*C)`

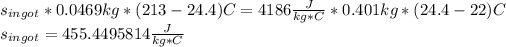
Therefore the specific heat of the ingot is 455(J/kg*°C)