Question

Type the correct answer in each box. Use numerals instead of words. If necessary, use / for the fraction bar(s).

Answer 1

2x for upper rectangle, 3 for lower rectangle.

Explanation:

y=2x , the slope = 2 if -3≤x<0

y=3 1/2<x<3/2

Answer 2

Piecewise function:

`f(x)=\left\{\begin{matrix}2x &\ \ \ \text{ if }-3\leq x<0\\3&\ \ \ \text{ if }(1)/(2)<x<(3)/(2)\end{matrix}\right.`

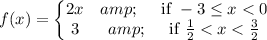
Explanation:

Given: Piece wise function graph.

We need to find the function.

In graph we can see two piece

For -3≤x≤0

End points on graph (-3,-6) and (0,0)

`y-0=(6)/(3)(x-0)`

`y=2x`

`\text{For } (1)/(2)<x<(3)/(2)`

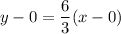
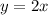
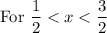
It is horizontal line. The equation of horizontal line is y=k.

Equation: y=3

Now, we write as piecewise function.

`f(x)=\left\{\begin{matrix}2x &\ \ \ \text{ if }-3\leq x<0\\3&\ \ \ \text{ if }(1)/(2)<x<(3)/(2)\end{matrix}\right.`

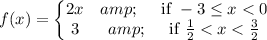
First blank = 2x

Second Blank = 3