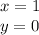Answer:
Option C (1, 0)
Explanation:
We have a system with the following equations:
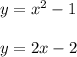
The first equation is a parabola.
The second equation is a straight line
To solve the system, substitute the second equation in the first and solve for x.
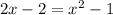
Simplify
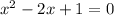
You must search for two numbers that when you add them, obtain as a result -2 and multiplying both results in 1.
These numbers are -1 and -1
Therefore
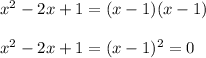
Finally the solutions are