Question

The proof that UX ≅ SV is shown. Given: △STU an equilateral triangle ∠TXU ≅ ∠TVS Prove: UX ≅ SV What is the missing statement in the proof? Statement Reason 1. ∠TXU ≅ ∠TVS 1. given 2. ∠STV ≅ ∠UTX 2. reflex. prop. 3. △STU is an equilateral triangle 3. given 4. ST ≅ UT 4. sides of an equilat. △ are ≅ 5. ? 5. AAS 6. UX ≅ SV 6. CPCTC

Answer 1

Triangle STU is congruent to triangle UTX is the missing step. AAS (angle-angle-side) is a method of proving 2 triangles congruent, and using the already proved information, you can find the triangles that are congruent by AAS.

Answer 2

5. Statement:
`\triangle TXU\cong \triangle TSV`

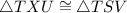
Explanation:

Given, triangle STU is an equilateral triangle.

`\angle TXU \cong \angle TVS`

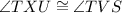
To prove that
`UX \cong SV`

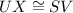
Proof:

1. Statement:
`\angle TXU \cong \angle TVS`

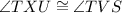
Reason: Given in question .

2. Statement:
`\angle STV \cong \angle UTX`

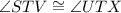
Reason: By using reflection proeperty of rotation.

3. Statement:
`\triangle STU` is an equilateral triangle.

Reason:
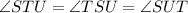`\angle STU= \angle TSU=\angle SUT` given.

4. Statement:
`ST \cong UT`

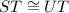
Reason: Sides of equilateral triangle STU.

5.
`\tringle TXU \cong \triangle TSV`

Reason: AAS congruence property of triangle.

6. Statement:
`UX\cong SV`

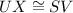
Reason: CPCT ( corresponding parts of congruence triangles).