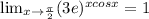Question

Find the limit of the function by using direct substitution.

limit as x approaches quantity pi divided by two of quantity three times e to the x times cosine of x.
The choices are:
a. 1
b. pi/2
c. 0
d. 5e^(pi/2)

Answer 1

Option a.

`\lim_{x \to (\pi)/(2)}(3e)^(xcosx)=1`

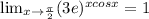
Explanation:

You have the following limit:

`\lim_{x \to (\pi)/(2){(3e)^(xcosx)`

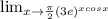
The method of direct substitution consists of substituting the value of
`(\pi)/(2)` in the function and simplifying the expression obtained.

We then use this method to solve the limit by doing
`x=(\pi)/(2)`

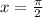
Therefore:

`\lim_{x \to (\pi)/(2)}{(3e)^(xcosx) = \lim_{x\to (\pi)/(2)}{(3e)^{(\pi)/(2)cos((\pi)/(2))}`

`cos((\pi)/(2))=0\\`

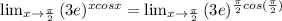
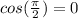
By definition, any number raised to exponent 0 is equal to 1

So

`\lim_{x\to (\pi)/(2)}{(3e)^{(\pi)/(2)cos((\pi)/(2))} = \lim_{x\to (\pi)/(2)}{(3e)^{(\pi)/(2)(0)}\\\\`

`\lim_{x\to (\pi)/(2)}{(3e)^(0)} = 1`

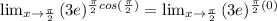
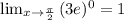
Finally

`\lim_{x \to (\pi)/(2)}(3e)^(xcosx)=1`