Question

Find the limit of the function by using direct substitution.

limit as x approaches quantity pi divided by 2 of quantity 2e^x sin x

The choices are:
a. 0
b. 2e^(pi/2)
c. 1
d. pi/2

Answer 1

The answer I would choose is b). Pi/2

Answer 2

b. 2e^(pi/2)

Explanation:

We have to evaluate the following expression by using direct substitution:

`\lim_{x \to (\pi)/(2) } 2e^(x) sin(x)`

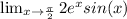
Substituting the value of x, we get:

`2e^{(\pi)/(2) } sin((\pi)/(2) )`

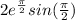
Since, the value of sin(π/2) = 1, the above expression will be reduced to:

`2e^{(\pi)/(2) }`

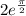
Therefore, option b gives the correct answer