Answer:
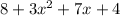
Explanation:
The first expression is
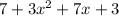
The sum of the constants is 7+3=10
The sum of the coefficients is 3+7=10
The second expression is;
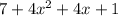
The sum of the constants is 7+1=8
The sum of the coefficients is 4+4=8
The third expression is;
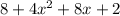
The sum of the constants is 8+2=10
The sum of the coefficients is 4+8=12
The fourth expression is;
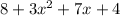
The sum of the constants is 8+4=12
The sum of the coefficients is 3+7=10
Hence the correct choice is the expression in which the sum of the constants greater than the sum of the coefficients