Answer:
D. 10
Explanation:
To find the distance between two points, use the distance formula:
Distance between two points
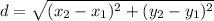
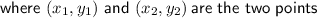
Define the two points:
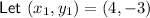
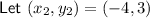
Substitute the two defined points into the distance formula and solve for d:
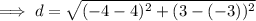
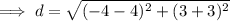
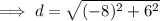
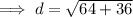
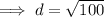
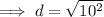
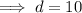
Therefore, the distance between the two given points is 10 units.