Answer:
Option C
Explanation:
When you rotate a point you could rotate it in Clockwise direction because that's how the hand of a clock move, or rotate it in Counterclockwise direction that's the opposite rotation. In math, counterclockwise is defined as being a positive rotation while clockwise is defined as being a negative rotation. Rotating a whole shape means we're rotating every point in the shape.
On the coordinate plane, consider the point (x,y). To rotate this point by 90° around the origin in counterclockwise direction, you can always swap the x- and y-coordinates and then multiply the new x-coordinate by -1. In a mathematical language this is as follows:
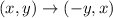
By applying this rule to every point we have:
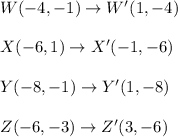
The figure below shows the original shape in green while the rotated shape is the one in red. As you can see, this figure matches the option C.