Answer:
26042.
Explanation:
What's the first term of this geometric series?
2.
What's the common ratio of this geometric series?
Divide one of the terms with the previous term. For example, divide the second term -10 with the first term 2.
 .
.
What's the sum of this series to the seventh term?
The sum of the first n terms of a geometric series is:
 ,
,
where
 is the first term of the series,
is the first term of the series,
 is the common ratio of the series, and
is the common ratio of the series, and
 is the number of terms in this series.
is the number of terms in this series.
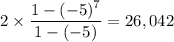 .
.