Question

Find the area of the yellow region. Round to the nearest tenth.

Answer 1

You have a square and four quarter circles with a radius of 4.

The area is

`{ 8}^(2) - 4 * (90)/(360) \pi * {4}^(2) \\ = 64 - 4 * (1)/(4) \pi * 16 \\ = 64 - \pi * 16`

Put that into your calculator and get the answer.

Answer 2

The area of yellow region is:

13.8 cm^2

Explanation:

The area of the yellow region is the area of square minus 4 times the area of one half semicircle at the corner of the square.

These four half semicircle will form a complete circle.

This means that the area of 4 half semicircles is equal to the area of the circle.

Hence, the area of yellow region is:

Area of square-Area of circle of radius 4 cm.

Also, the radius(r) of circle is: 4 cm.

and the area of circle is given by:
`\pi r^2`

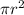
i.e.

`Area\ of\ circle=3.14* 4^2\\\\i.e. \\\\Area\ of\ circle=50.24\ cm^2`

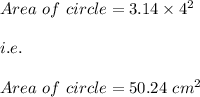
Area of square is:
`s^2`

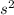
where s is the side length of the square.

Here

`s=8\ cm.`

Hence,

`Area\ of\ square=8^2\\\\Area\ of\ square=64\ cm^2`

Hence, Area of yellow region is:

`=64-50.24\\\\=13.76\ cm^2`

which to the nearest tenth is: 13.8 cm^2