Question

A cylinder and a rectangular prism have the same volume and the same height the base of the prism is a square with a side length of 9 cm

what is the approximate radius of the cylinder?

A. 4.5 cm

B. 5.1 cm

C. 12.9 cm

D. 25.8 cm

Answer 1

B. 5.1 cm

Explanation:

Formula to calculate volume of prism with base of a square

V = l²(h)

where l is side of square

h is height of prism

Formula to calculate volume of cylinder

V = πr² h

Given in the question that both have same volume and height so we will equate their volume

Equation

l²(h) = πr² h

and

plug given values in the variable

9²(h) = πr² h

height will cancel out

81 = πr²

r² = 81/π

r = √81/π

r = 5.08 cm

r ≈ 5.1 cm

Answer 2

Answer: Option B

Explanation:

The formula of the volume of a cylinder is:

`V=\pi r^2h`

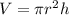
Where the radius is "r" and the height is "h".

The formula of the volume of a rectangular prism is:

`V=Ah`

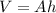
Where "A" is the area of the base and "h" is the heigth.

As both volumes are equal, you can write:

`V=V\\\pi r^2h=Ah`

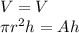
Find the area of the base, which is a square, with the formula:

`A=s^2`

Where "s" is the lenght of any side of the square.

`A=(9cm)^2=81cm^2`

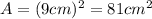
Divide both sides of the equation by "h" (because the heights are equal) and solve for the radius:

`(\pi r^2h)/(h)=(Ah)/(h)`

`\pi r^2=81cm^2\\\\r=\sqrt{(81cm^2)/(\pi)}`

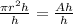
`r=5.07cm`≈5.1 cm