Question

Solve for p. 2(p+ 5) = 16

Solve for t. -3(t + 1) = 18

Solve for x -2/5 (x+10)=-10

Solve for x. 2/3 (x -10)=-2

Answer 1

Hello!

The answers are:

1
`p=3`

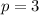
2
`x=-7`

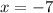
3
`x=35`

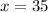
4
`x=7`

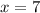
Why?

To know the solution of the problems, we need to isolate each variable.

Remember that:

- If we have an equality: if the number is part of a product , and if you need to move it to the other side of the equality, the same number will be dividing the factors of the side.

- If we have an equality: if the number is subtracting (negative sign), and if you need to move it to the other side of the equality, its sign changes to positive.

- If we have an equality: if the number is adding (positive sign), and if you need to move it to the other side of the equality, its sign changes to negative.

- The distributive property states that:

`a(b+c)=ab+ac`

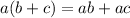
So,

1 - Solving for p

`2(p+5)=16\\2p+10=16\\2p=16-10=6\\p=(6)/(2)=3`

2 - Solving for t

`-3(t+1)=18\\-3t-3=18\\-3t=18+3=21\\t=(21)/(-3)=-7`

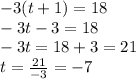
3 - Solving for x

`-(2)/(5)(x-10)=-10\\-(2)/(5)x+(2)/(5) *10=-10\\-(2)/(5)x+4=-10 \\-(2)/(5)x=-10-4=-14\\-(2)/(5)x=-14\\x=(-14)/((-2)/(5) )=14*(5)/(2)=35`

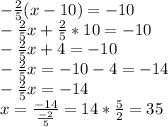
4 - Solving for x

`(2)/(3)(x-10)=-2\\\\x-10=(-2)/((2)/(3) )=-2*(\\3)/(2)\\\\x-10=-3\\x=-3+10\\x=7`

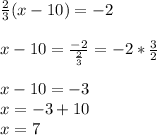
Have a nice day!

Answer 2

1)
`p=3`

2)
`t=-7`

3)
`x=15`

4)
`x=7`

Explanation:

1) Apply distributive property:

`2(p+ 5) = 16\\2p+10=16`

Subtract 10 from both sides of the equation and then divide both sides by 2:

`2p+10-10=16-10\\(2p)/(2)=(6)/(2)\\p=3`

2) Apply distributive property:

`-3(t + 1) = 18\\-3t -3= 18`

Add 3 to both sides of the equation and then divide both sides by -3:

`-3t -3+3= 18+3\\(-3t)/(-3)=(21)/(-3)\\t=-7`

3) Apply distributive property:

`-(2)/(5)(x+10)=-10\\\\-(2)/(5)x-4=-10`

Add 4 to both sides of the equation:

`-(2)/(5)x-4+4=-10+4\\\\-(2)/(5)x=-6`

Multiply both sides by
`-(5)/(2)`:

`(-(2)/(5)x)(-(5)/(2)) =-6(-(5)/(2))\\\\x=15`

4) Apply distributive property:

`(2)/(3)(x-10)=-2\\\\(2)/(3)x-(20)/(3)=-2`

Add
`(20)/(3)` to both sides of the equation:

`(2)/(3)x-(20)/(3)+(20)/(3)=-2+(20)/(3)\\\\(2)/(3)x=(14)/(3)`

Multiply both sides by
`(3)/(2)`:

`((2)/(3)x)((3)/(2))=((14)/(3))((3)/(2))\\\\x=7`