Hello!
The answer is:
The last option,
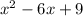
Why?
The area of square is given by the following formula:
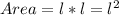
Where, l is the side of the square, remember that a square has equal sides.
To solve the problem, we must remember the following notable product:
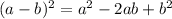
So, if the side of the given circle is (x-3), the area will be:
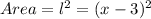
Applying the notable product, we have:
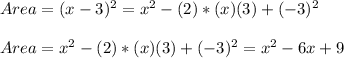
So, the correct option is the last option:
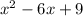
Have a nice day!