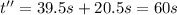Question

A rocket rises vertically, from rest, with an acceleration of 3.6m/s^2 until it runs out of fuel at an altitude of 1500m. After this point, its acceleration is that of gravity, downward. A. What is the velocity of the rocket when it runs out of fuel? B. How long does it take to reach this point? C.What maximum altitude does the rocket reach? D. How much time (total) does it take to reach maximum altitude? E.With what velocity does the rocket strike the Earth? F.How long (total) is it in the air?

Answer 1

A. 103.9 m/s

The motion of the rocket until it runs out of fuel is an accelerated motion with constant acceleration a = 3.6 m/s^2, so we can use the following equation

`v^2 -u^2 = 2ad`

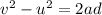
where

v is the velocity of the rocket when it runs out of fuel

u = 0 is the initial velocity of the rocket

a = 3.6 m/s^2 is the acceleration

d = 1500 m is the distance covered during this first part

Solving for v, we find

`v=√(u^2+2ad)=√((0^2+2(3.6 m/s^2)(1500 m))=103.9 m/s`

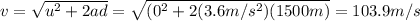
B. 28.9 s

We can calculate the time taken for the rocket to reach this altitude with the formula

`d=(1)/(2)at^2`

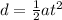
where

d = 1500 m

a = 3.6 m/s^2

Solving for t, we find

`t=\sqrt{(2d)/(a)}=\sqrt{(2(1500 m))/(3.6 m/s^2)}=28.9 s`

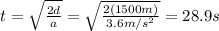
C. 2050.8 m

We can calculate the maximum altitude reached by the rocket by using the law of conservation of energy. In fact, from the point it runs out of fuel (1500 m above the ground), the rocket experiences the acceleration due to gravity only, so all its kinetic energy at that point is then converted into gravitational potential energy at the point of maximum altitude:

`K_i = U_f\\(1)/(2)mu^2 = mgh`

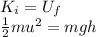
where h is distance covered by the rocket after it runs out of fuel, and v=103.9 m/s is the velocity of the rocket when it starts to decelerate due to gravity. Solving for h,

`h=(v^2)/(2g)=((103.9 m/s)^2)/(2(9.8 m/s^2))=550.8 m`

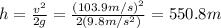
So the maximum altitude reached by the rocket is

`h' = d+h=1500 m +550.8 m=2050.8 m`

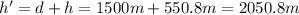
D. 39.5 s

The time needed for the second part of the trip (after the rocket has run out of fuel) can be calculated by

`h=(1)/(2)gt^2`

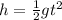
where

h = 550.8 m is the distance covered in the second part of the trip

g = 9.8 m/s^2

Solving for t,

`t=\sqrt{(2h)/(g)}=\sqrt{(2(550.8 m))/(9.8 m/s^2)}=10.6 s`

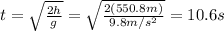
So the total time of the trip is

`t'=28.9 s+10.6 s=39.5 s`

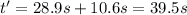
E. 200.5 m/s

When the rocket starts moving downward, it is affected by gravity only. So the gravitational potential energy at the point of maximum altitude is all converted into kinetic energy at the instant the rocket hits the ground:

`(1)/(2)mv^2 = mgh`

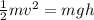
where

v is the final velocity of the rocket

h = 2050.8 m is the initial altitude of the rocket

Solving for v,

`v=√(2gh)=√(2(9.8 m/s^2)(2050.8 m))=200.5 m/s`

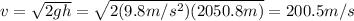
F. 60 s

We need to calculate the time the rocket takes to fall down to the ground from the point of maximum altitude, and that is given by

`h'=(1)/(2)gt^2`

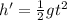
where

h' = 2050.8 m

g = 9.8 m/s^2

Solving for t,

`t=\sqrt{(2h')/(g)}=\sqrt{(2(2050.8 m))/(9.8 m/s^2)}=20.5 s`

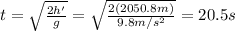
So the total time of the trip is

`t''=39.5 s+20.5 s=60 s`