Question

asked Aug 26, 2020 52.5k views

2 Answers

Eman · Answer 1 · 2020-08-28T17:57:50+0000

Hello!

The answer is:

The equation of the given circle is:

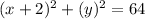
(x+2)^(2) +(y)^(2)=64

The equation of a circle is given by the following equation:

(x-h)^(2) +(y-k)^(2)=r^(2)

We are given the center point (-2,0) and the area of the circle.

The area of a circle is given by the formula:

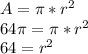
$A=\pi*r^(2)\\64\pi=\pi*r^(2)\\64=r^(2)$

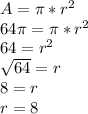
$A=\pi*r^(2)\\64\pi=\pi*r^(2)\\64=r^(2)\\√(64)=r\\8=r\\r=8$

So, the radius of the circle is 8 units.

Therefore,

We are given a circle where:

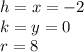
$h=x=-2\\k=y=0\\r=8$

Then, substituting into the circle equation, we have:

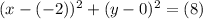
(x-(-2))^(2) +(y-0)^(2)=(8)^

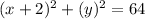
(x+2)^(2) +(y)^(2)=64

Hence, the simplified equation of the circle is:

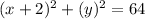
(x+2)^(2) +(y)^(2)=64

Have a nice day!

Siddharth Srivastava · Answer 2 · 2020-08-31T07:25:28+0000

Answer:

The required equation in standard form is
(x+2)^2+y^2=64

Explanation:

The equation of a circle with center (h,k) an radius, r units is given by the formula;

(x-h)^2+(y-k)^2=r^2

The given circle has center (-2,0) and radius squared can be calculated from the given area, which is
$64\pi$

$\pi r^2=64\pi$

$\implies r^2=64$

We substitute these values into the formula to obtain;

(x--2)^2+(y-0)^2=64

We simplify to get;

(x+2)^2+y^2=64