Answer:
A. The maximum height of the ball is about 342 feet, which occurs approximately 4½ seconds after the ball is hit.
Explanation:
The height of the ball is demonstrated by the equation:
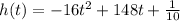
The given equation is a quadratic equation. The maximum/minimum of a quadratic equation occurs at the vertex.
The vertex of a general quadratic equation of the form:
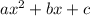
occurs at x =
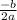
Comparing the given equation with general equation, we get:
a = -16
b = 148
So, the maximum value will occur when t will be:
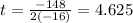
From the given options we can see that the closest to 4.625 is 4
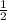 which is given by option A.
which is given by option A.
So from here we can conclude that : The maximum height of the ball is about 342 feet, which occurs approximately 4½ seconds after the ball is hit.