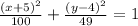Question

What is the standard form equation of the ellipse that has vertices (-15, 4) and (5, 4) and co-vertices (-5, -3) and

(-5, 11)?

Answer 1

Explanation:

Notice that the main vertices (-15,4) and (5,4) both have the same y coordinate. This means that the focal axis is horizontal so we have a horizontal ellispe.

Equation of a horizontal ellipse is

`\frac{(x - h) {}^(2) }{ {a}^(2) } + \frac{(y - k) {}^(2) }{ {b}^(2) } = 1`

I'll explain the variables.

Step 1: Find the center.

The center (h,k) is the midpoint of either the main or co vertices. It doesn't matter because of the definition of an ellipse.

So using the midpoint formula, let find the midpoint of the main vertices.

`( ( - 15 + 5)/(2) ) = - 5`

`(4 + 4)/(2) = 4`

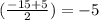
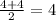
So our center is (-5,4) so as of right now we have

`\frac{(x + 5) {}^(2) }{ {a}^(2) } + \frac{(y - 4) {}^(2) }{ {b}^(2) } = 1`

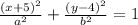
Step 2: The variable a represents the semi major axis. This

basically means what is the distance from the center to either main vertex.

Here, let use (5,4). Using (5,4), our main vertex and (-5,4), our center.

Use the distance formula

`a= \sqrt{(5 - ( - 5) {}^(2) + (4 - 4) {}^(2) }`

`a = √(100)`

`a= 10`

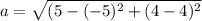
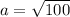
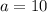
So our distance is 10, this means a=10

Step 3: The variable b represent the semi minor axis. This basically the distance from the center to either co vertex.

Using the distance formula,

`b = \sqrt{ (- 5 - ( - 5) {}^(2) + (4 - 11) {}^(2) }`

`b = √(49)`

`b = 7`

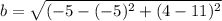
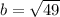
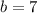
So b=7, so finally we plug a=10, b=7

`\frac{(x + 5) {}^(2) }{100} + \frac{(y - 4) {}^(2) }{49} = 1`