To find the length of a segment you can use the pythagorean theorem: given two points
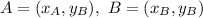 you have
you have

In your case, we have

Note that your exercise seems to suggest the opposite, i.e.
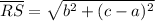
Don't worry: the two numbers are the same. In fact,
 and
and
 are opposite, and opposite numbers are the same when squared (for example,
are opposite, and opposite numbers are the same when squared (for example,
 )
)
It had to be so after all: we're simply claiming that the distance between R and S or between S and R is the same..how could it be any different?