Question

Anyone know how to do this?

Answer 1

The height is
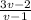`(3v-2)/(v-1)` ⇒ answer (A)

Explanation:

* To solve this problem you must know how to factorize a

trinomial and how to find the volume of the prism

* To factor a trinomial in the form x² ± bx ± c:

- Look at the c term first.

# If the c term is a positive number, then the factors of c will both be positive or both be negative. In other words, r and s will have the same sign and find two integers, r and s, whose product is c and whose sum is b.

# If the c term is a negative number, then one factor of c will be positive, and one factor of c will be negative. Either r or s will be negative, but not both.and find two integers, r and s, whose product is c and whose difference is b.

- Look at the b term second.

# If the c term is positive and the b term is positive, then both r and s are positive.

Ex: x² + 5x + 6 = (x + 3)(x + 2)

# If the c term is positive and the b term is negative, then both r and s are negative.

Ex: x² - 5x + 6 = (x -3)(x - 2)

# If the c term is negative and the b term is positive, then the factor that is positive will have the greater absolute value. That is, if |r| > |s|, then r is positive and s is negative.

Ex: x² + 5x - 6 = (x + 6)(x - 1)

# If the c term is negative and the b term is negative, then the factor that is negative will have the greater absolute value. That is, if |r| > |s|, then r is negative and s is positive.

Ex: x² - 5x - 6 = (x - 6)(x + 1)

* Now lets revise the volume of the prism

- The volume of the prism = area of its base × its height

* To find the height divide the volume by the area of the base

∵ The volume of the prism =
`(3v^(2)-19v-14)/(3v^(2)-v-2)`

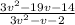
- Factorize the two trinomials completely:

# 3v² - 19v - 14 ⇒ 3v² = 3v × v ⇒ 14 = 2 × 7

∵ 3v × 7 = 21v

∵ v × 2 = 2v

∵ 21 > 2

∴ the sign of 21v is -ve and the sign of 2v is +ve

∵ -21v + 2v = -19v

∴ 3v² - 19v - 14 = (3v + 2)(v - 7)

# 3v² - v - 2 ⇒ 3v² = 3v × v ⇒ 2 = 2 × 1

∵ 3v × 1 = 3v

∵ v × 2 = 2v

∵ 3 > 2

∴ the sign of 3v is -ve and the sign of 2v is +ve

∵ -3v + 2v = -v

∴ 3v² - v - 2 = (3v + 2)(v - 1)

∴
`V=((3v+2)(v-7))/((3v+2)(v-1))`

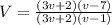
* Now simplify the fraction by canceling the like terms from up and down

∴ We will cancel (3v + 2) up with (3v + 2) down

∴
`V = ((v-7))/((v-1))`

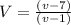
* Lets find the area of the base

∵ The base is a rectangle with dimensions:

`L=((v-7))/((3v+2)),W=((3v+2))/((3v-2))`

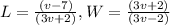
∵ Area the rectangle = L × W

∴
`A=((v-7))/((3v+2))*((3v+2))/((3v-2))=((v-7))/((3v-2))`

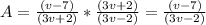
- We canceled (3v + 2) up with (3v + 2) down

∵ h = V ÷ A

∴
`h=((v-7))/((v-1))` ÷
`((v-7))/((3v-2))`

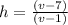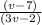
* Change the division sign by multiplication sign and reciprocal

the fraction after the division sign

∴
`h= ((v-7))/((v-1))` ×
`((3v-2))/((v-7))=((3v-2))/((v-1))`

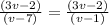
- We canceled (v - 7) up with (v - 7) down

∴ The answer is (A)

Answer 2

Option A)

`h=((3v-2))/((v-1))`

Explanation:

Remember that the volume of a rectangle is:

`V = lwh`

Where l is the length, w is the width and h is the height.

In the figure, these three dimensions are given as a function of the variable v.

Then the volume will be the product of the three expressions.

If we have the volume, the width and the length of the rectangle, then we find the height when we divide the volume by the product of the width and the length

`h = (V)/((lw))`

The volume is:

`V=(3v^2-19v-14)/(3v^2-v-2)`

The product of the width and the length is:

`lw=(v-7)/(3v+2)*(3v+2)/(3v-2)\\\\lw=(v-7)/(3v-2)`

Now

`h=(V)/(lw)=((3v^2-19v-14)/(3v^2-v-2))/((v-7)/(3v-2))\\\\\\h=(3v^2-19v-14(3v-2))/(3v^2-v-2(v-7))`

we factor quadratic expressions

`3v^2-19v-14\\a=3\\b=-19\\c=-14\\`

We use the quadratic formula to factor the expression

`3v^2-19v-14\\\\v_1 =(19+√(19^2-4(3)(-14)))/(2(3))\\\\v_2=(19-√(19^2-4(3)(-14)))/(2(3))\\\\v_1=7\\\\v_2=-(2)/(3)\\\\3v^2-19v-14 = (v-7)(3v+2)`

We also factor the quadratic function
`3v^2-v-2` using the quadratic formula

`3v^2-v-2\\\\a=3\\\\b=-1\\\\c=-2\\\\v_1 =(1+√(1^2 -4(3)(-2)))/(2(3))\\\\v_2=(1-√(1^2 -4(3)(-2)))/(2(3))\\\\v_1=1\\\\v_2=-(2)/(3)\\\\3v^2-v-2 = (v-1)(3v+2)`

So the height is

`h=((v-7)(3v+2)(3v-2))/((v-1)(3v+2)(v-7))\\\\h=((3v-2))/((v-1))`