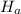Answer:
Therefore we fail to reject the Null hypothesis
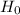
Because the is no sufficient evidence to support the claim of the alternative hypothesis
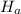
Explanation:
From the question we are told that
Sample size
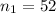
Mean time 1
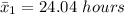
Mean time 2

Standard deviation
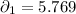
Standard deviation
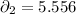
Level of significance 0.05
The null hypothesis is
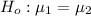
Alternative hypothesis
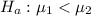
Generally the test statistics is mathematically represented as

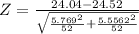
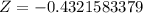

From Table the Z-critical value at
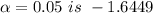
Therefore
Zcal> Zcritical
(-0.43)=(-1.645)
Generally we fail to reject the null hypothesis
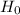 at
at
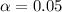
Therefore we fail to reject the
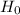
Because the is no sufficient evidence to support the claim of