Answer:
1.314 MJ
Explanation:
As water is removed from the tank, decreasing amounts are raised increasing distances. The total work done is the integral of the work done to raise an incremental volume to the required height.
There are a couple of ways this can be figured. The "easy way" involves prior knowledge of the location of the center of mass of a cone. Effectively, the work required is that necessary to raise the mass from the height of its center to the height of the discharge pipe.
The "hard way" is to write an expression for the work done to raise an incremental volume, then integrate that over the entire volume. Perhaps this is the method expected in a Calculus class.
Mass of water
The mass of the water being raised is the product of the volume of the cone and the density of water.
The cone volume is ...
V = 1/3πr²h . . . . . . for radius 2 m and height 8 m
V = 1/3π(2 m)²(8 m) = 32π/3 m³
The mass of water in the cone is then ...
M = density × volume
M = (1000 kg/m³)(32π/3 m³) ≈ 3.3510×10^4 kg
Center of mass
The center of mass of a cone is 1/4 of the distance from the base to the point. In this cone, it is (1/4)(8 m) = 2 m from the base.
Easy Way
The discharge pipe is 2 m above the base of the cone, so is 4 m above the center of mass. The work required to lift the mass from its center to a height of 4 m above its center is ...
W = Fd = (9.8 m/s²)(3.3510×10^4 kg)(4 m) = 1.3136×10^6 J
Hard Way
As the water level in the conical tank decreases, the remaining volume occupies a space that is similar to the entire cone. The scale factor is the ratio of water depth to the height of the tank: (y/8). The remaining volume is the total volume multiplied by the cube of the scale factor.
V(y) = (32π/3)(y/8)³
The differential volume at height y is the derivative of this:
dV = π/16y²
The work done to raise this volume of water to a height of 10 m is ...
(9.8 m/s²)(1000 kg/m³)(dV)((10 -y) m) = 612.5π(y²)(10 -y) J
The total work done is the integral over all heights:
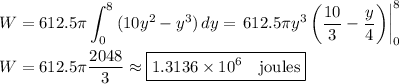
It takes about 1.31 MJ of work to empty the tank.